Why is the beta coefficient from 0.3 to 0.7?
Where can we get the beta orifice of numbers and how important are they to keep the Orifice Beta ratio in aperture calculations ?between 0.3 and 0.7?
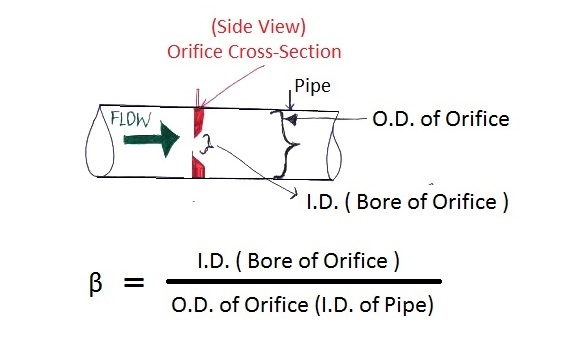To understand the purpose. Let’s rebel.
What happens if we take the beta coefficient to be 1?
If ID from orifice = OD from Orifice is possible, this is possible
But this means that there is no limit to the flow so there is no pressure drop.
And no pressure drop is therefore possible to measure the flow
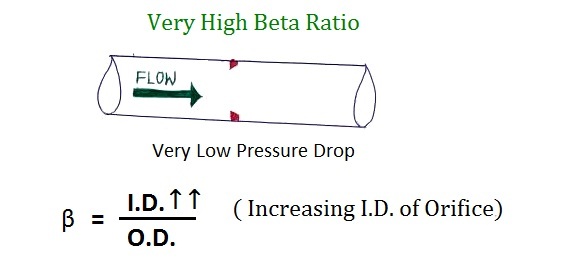
What if we set the beta to 0.9?
This is possible if the ID from the aperture is approximately close to the OD of the orifice
But this means that there are very few restrictions on the flow of very low pressure drops.
And measuring pressure drop is very difficult so we will not go beyond 0.7
Also “unreliable increase”, this concept is explained below
What happens if we take the beta coefficient to 0.1?
This is possible if the ID from the orifice is very small compared to the OD from the Orifice
But this means that there is a very high limit to the pressure drop.
this is good? Strong pressure drop means it will be easy to measure? This is not our only concern !! Affects these cases (some reasons mentioned below)
Hydraulic process
This affects the hydraulic calculation of the process and also leads to process inefficiencies.
As PUMP have to PUMP more! The result is people processing on their data page
Determine the maximum allowable pressure drop in the orifice.
What good is a web site if it simply “blends in” with everything else out there?
More likely cavitation and flushing
The lower the pressure, the more likely it is for liquids to reach “vapor pressure”.
And so there is a better chance of “cavitation and flushing”
Unloading coefficient (uncertainty)
Estimated uncertainty of experimental discharge coefficient for concentrate, square, flange edge meters that comply with this standard (API 14.3.1)
It is a function of the Reynolds number and the diameter ratio (β).
In the very large Reynolds number (approximately greater than 1,000,000) the uncertainty is only a function of the diameter ratio (BETA) (β).
So this is where the beta ratio comes in again
Below is Figure 14.3.1 of the API Standards, which has a percentage uncertainty versus Beta Ratio
(Look at the comments in red)
So from this graph we can conclude that it is better to get an average value on average for better accuracy
Reach BETA = 0.0 !! The end of an unanswered question?
Why should the beta be between 0.3 and 0.7?
There is no hard and fast rule, it is only for the above reasons that we want to stay moderate, this limit is set by the “experimental” method (that is, we have reached this value by experiment).
Some standards say we should be between 0.2 and 0.6
None less, stay safe and choose a moderate amount Thank you for reading
Rose Calibration Company in Melbourne, Australia with over ten years of experience provides all calibration, maintenance, and repair services throughout Australia. If you live in Sydney, Melbourne, Adelaide, Perth, Geelong, and Brisbane, you can receive your quote in less than two hours by fill-up the form via the “Booking” link.
